- Geometric squeezing of rotating quantum gases into the lowest Landau level (9/5/2023)
Valentin Crépel, Ruixiao Yao, Biswaroop Mukherjee, Richard J. Fletcher, Martin Zwierlein
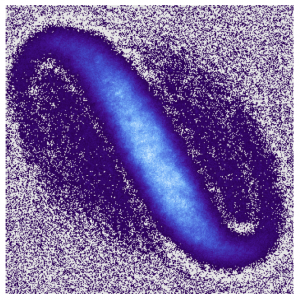
The simulation of quantum Hall physics with rotating quantum gases is witnessing a revival due to recent experimental advances that enabled the observation of a Bose-Einstein condensate entirely contained in its lowest kinetic energy state, i.e. the lowest Landau level. We theoretically describe this experimental result, and show that it can be interpreted as a squeezing of the geometric degree of freedom of the problem, the guiding center metric. This “geometric squeezing” offers an unprecedented experimental control over the quantum geometry in Landau-level analogues, and at the same time opens a realistic path towards achieving correlated quantum phases akin to quantum Hall states with neutral atoms.
- Observation of chiral edge transport in a rapidly-rotating quantum gas (4/20/2023)
Observation of chiral edge transport in a rapidly-rotating quantum gas
Ruixiao Yao, Sungjae Chi, Biswaroop Mukherjee, Airlia Shaffer, Martin Zwierlein, Richard J. Fletcher
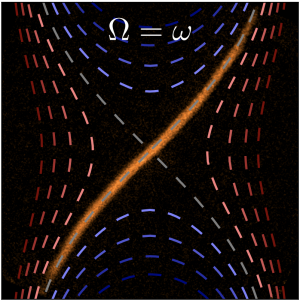
The frictionless, directional propagation of particles at the boundary of topological materials is one of the most striking phenomena in transport. These chiral edge modes lie at the heart of the integer and fractional quantum Hall effects, and their extraordinary robustness against noise and disorder reflects the quantization of Hall conductivity in these systems. Despite their central importance, controllable injection of edge modes, and direct imaging of their propagation, structure, and dynamics, is challenging. Here, we demonstrate the distillation of individual chiral edge states in a rapidly-rotating bosonic superfluid confined by an optical boundary. Tuning the wall sharpness, we reveal the smooth crossover between soft wall behaviour in which the propagation speed is proportional to wall steepness, and the hard wall regime exhibiting chiral free particles. From the skipping motion of atoms along the boundary, we spectroscopically infer the energy gap between the ground and first excited edge bands, and reveal its evolution from the bulk Landau level splitting for a soft boundary, to the hard wall limit.
- Crystallization of Bosonic Quantum Hall States (1/5/2022)
Biswaroop Mukherjee, Airlia Shaffer, Parth B. Patel, Zhenjie Yan, Cedric C. Wilson, Valentin Crépel, Richard J. Fletcher, Martin W. Zwierlein
Nature 601, 58-62 (2022) download
Featured in MIT News, Smithsonian Magazine, Popular Science, and on the Apple News feed
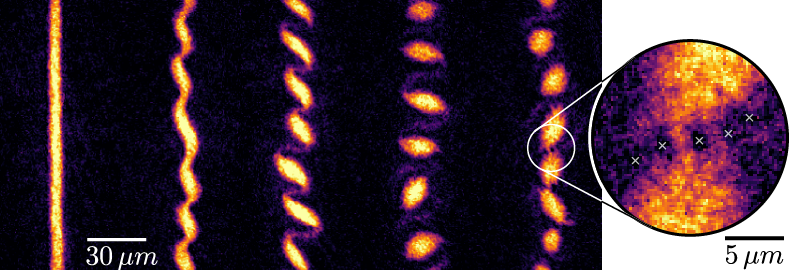
The dominance of interactions over kinetic energy lies at the heart of strongly correlated quantum matter, from fractional quantum Hall liquids, to atoms in optical lattices and twisted bilayer graphene. Crystalline phases often compete with correlated quantum liquids, and transitions between them occur when the energy cost of forming a density wave approaches zero. A prime example occurs for electrons in high magnetic fields, where the instability of quantum Hall liquids towards a Wigner crystal is heralded by a roton-like softening of density modulations at the magnetic length. Remarkably, interacting bosons in a gauge field are also expected to form analogous liquid and crystalline states. However, combining interactions with strong synthetic magnetic fields has been a challenge for experiments on bosonic quantum gases. Here, we study the purely interaction-driven dynamics of a Landau gauge Bose-Einstein condensate in and near the lowest Landau level (LLL). We observe a spontaneous crystallization driven by condensation of magneto-rotons, excitations visible as density modulations at the magnetic length. Increasing the cloud density smoothly connects this behaviour to a quantum version of the Kelvin-Helmholtz hydrodynamic instability, driven by the sheared internal flow profile of the rapidly rotating condensate. At long times the condensate self-organizes into a persistent array of droplets, separated by vortex streets, which are stabilized by a balance of interactions and effective magnetic forces.
- Geometric squeezing into the lowest Landau level (6/18/2021)
Richard J. Fletcher, Airlia Shaffer, Cedric C. Wilson, Parth B. Patel, Zhenjie Yan, Valentin Crépel, Biswaroop Mukherjee, Martin W. Zwierlein
Science 18 Jun 2021:
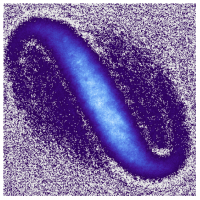
Vol. 372, Issue 6548, pp. 1318-1322The physics of rotation plays a fundamental role across all physical arenas, from nuclear matter, to weather patterns, star formation, and black holes. The behaviour of neutral objects in a rotating frame is equivalent to that of charged particles in a magnetic field, which exhibit intriguing transport phenomena such as the integer and fractional quantum Hall effects. An intrinsic feature of both these systems is that translations along different directions do not commute, implying a Heisenberg uncertainty relation between spatial coordinates. This underlying non-commutative geometry plays a crucial role in quantum Hall systems, but its effect on the dynamics of individual wavefunctions has not been observed. Here, we exploit the ability to squeeze non-commuting variables to dynamically create a Bose-Einstein condensate in the lowest Landau level (LLL). We directly resolve the extent of the zero-point cyclotron orbits, and demonstrate geometric squeezing of the orbits’ guiding centres by more than 7 dB below the standard quantum limit. The condensate attains an aspect ratio exceeding 100 and an angular momentum of more than 1000ℏ per particle. This protocol naturally prepares a condensate in which all atoms occupy a single Landau gauge wavefunction in the LLL, with an interparticle distance approaching the size of the cyclotron orbits, offering a new route towards strongly correlated fluids and bosonic quantum Hall states.
- Congratulations to Dr. Richard Fletcher on his Assistant Professorship at MIT (3/29/2020)
We are all excited for Rich to be starting his own research group at MIT!
Riddle:
How do you go from this:
to this: